Free Online Productivity Tools
i2Speak
i2Symbol
i2OCR
iTex2Img
iWeb2Print
iWeb2Shot
i2Type
iPdf2Split
iPdf2Merge
i2Bopomofo
i2Arabic
i2Style
i2Image
i2PDF
iLatex2Rtf
Sci2ools
CVPR
2007
IEEE
2007
IEEE
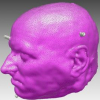
Delaunay Deformable Models: Topology-Adaptive Meshes Based on the Restricted Delaunay Triangulation
In this paper, we propose a robust and efficient Lagrangian approach, which we call Delaunay Deformable Models, for modeling moving surfaces undergoing large deformations and topology changes. Our work uses the concept of restricted Delaunay triangulation, borrowed from computational geometry. In our approach, the interface is represented by a triangular mesh embedded in the Delaunay tetrahedralization of interface points. The mesh is iteratively updated by computing the restricted Delaunay triangulation of the deformed objects. Our method has many advantages over popular Eulerian techniques such as the level set method and over hybrid Eulerian-Lagrangian techniques such as the particle level set method: localization accuracy, adaptive resolution, ability to track properties associated to the interface, seamless handling of triple junctions. Our work brings a rigorous and efficient alternative to existing topology-adaptive mesh techniques such as Tsnakes.
Computer Vision | CVPR 2007 | Delaunay Deformable Models | Delaunay Tetrahedralization | Delaunay Triangulation | Level Set Method | Topology-adaptive Mesh Techniques |
| Added | 12 Oct 2009 |
| Updated | 28 Oct 2009 |
| Type | Conference |
| Year | 2007 |
| Where | CVPR |
| Authors | Jean-Philippe Pons, Jean-Daniel Boissonnat |
Comments (0)