Free Online Productivity Tools
i2Speak
i2Symbol
i2OCR
iTex2Img
iWeb2Print
iWeb2Shot
i2Type
iPdf2Split
iPdf2Merge
i2Bopomofo
i2Arabic
i2Style
i2Image
i2PDF
iLatex2Rtf
Sci2ools
ISBI
2004
IEEE
2004
IEEE
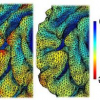
Diffusion Smoothing on Brain Surface via Finite Element Method
Surface data such as the segmented cortical surface of the human brain plays an important role in medical imaging. To increase the signal-to-noise ratio for data residing on the brain surface, the data is usually diffused. Most of diffusion equation approach for triangulated mesh data is based on the finite element method and a system of linear equations are iteratively solved without the explicit representation of the Laplace-Beltrami operator. Such implicit formulation requires inverting large sparse matrix that is required in most finite element methods. The novelty of our paper is in the explicit representation of the Laplace-Beltrami operator derived from the finite element method itself. The Laplace-Beltrami operator is expressed as a weighted averaging operator where the weights are expressed in terms of the interior angles and the area of triangles. The weights are computed by actually solving the system of linear equations in the finite element method and inverting a matrix i...
Finite Difference Scheme | Finite Element Method | Finite Element Methods | ISBI 2004 | Medical Imaging |
| Added | 20 Nov 2009 |
| Updated | 20 Nov 2009 |
| Type | Conference |
| Year | 2004 |
| Where | ISBI |
| Authors | Moo Chung, Jonathan Taylor |
Comments (0)