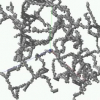
A geometric flow for white matter fibre tract reconstruction

In magnetic resonance diffusion tensor imaging (DTI), the direction and magnitude of diffusion of water molecules is characterized by a diffusion tensor. In the central nervous system, the highly organized fibre structure of white matter fibre tracts causes the diffusion to be anisotropic. From the DTI data, one can calculate a vector field representing the preferred direction of diffusion at each imaging voxel, which corresponds to the orientation of white matter fibres. However, the reconstruction of continuous fibre tracts from such data remains a challenge because the measurements are dense and typically quite noisy. In this paper we introduce a geometric flow to address this problem. The key ideas are: 1) to locally extend the vector field in its orthogonal plane and 2) to model the fibres as very thin tubes, by introducing a constraint on the minimum cross-sectional curvature. We illustrate the approach with reconstructions of both simulated and real diffusion tensor images.

• Type: Conference
• Year: 2002
• Where: ISBI
• Authors: Jennifer S. W. Campbell, Kaleem Siddiqi, Baba C. Vemuri, G. Bruce Pike
• Keywords: ISBI 2002, Matter Fibre Tracts, Medical Imaging, Real Diffusion Tensor, Resonance Diffusion Tensor