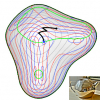
A linear formulation of shape from specular flow

When a curved mirror-like surface moves relative to its environment, it induces a motion field—or specular flow— on the image plane that observes it. This specular flow is related to the mirror’s shape through a non-linear partial differential equation, and there is interest in understanding when and how this equation can be solved for surface shape. Existing analyses of this ‘shape from specular flow equation’ have focused on closed-form solutions, and while they have yielded insight, their critical reliance on externally-provided initial conditions and/or specific motions makes them difficult to apply in practice. This paper resolves these issues. We show that a suitable reparameterization leads to a linear formulation of the shape from specular flow equation. This formulation radically simplifies the reconstruction process and allows, for example, both motion and shape to be recovered from as few as two specular flows even when no externally-provided initia...

• Type: Conference
• Year: 2009
• Where: ICCV
• Authors: Guillermo D. Canas, Yuriy Vasilyev, Yair Adato, Todd Zickler, Steven Gortler, Ohad Ben-Shahar
• Keywords: Computer Vision, ICCV 2009, Shape From Specular Flow