Multiresolution moment filters

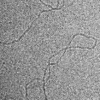
We define multi-scale moments that are estimated locally by analyzing the image through a sliding window at multiple scales. When the analysis window satisfies a two-scale relation, we prove that these moments can be computed very efficiently using a multiresolution wavelet-like algorithm. We also show that B-spline windows are best suited for this kind of analysis because, in addition to being refinable, they are positive, symmetric and very nearly isotropic. We present two applications of our method. The first is a feature extraction method for detecting strands of DNA in noisy cryoelectron-micrographs. The second is an extension of the LucasKanade optical flow algorithm that assumes a local affine model of the motion field. The results obtained in both cases are very promising.

• Type: Conference
• Year: 2002
• Where: ICIP
• Authors: Michael Sühling, Michael Unser, Muthuvel Arigovindan, Patrick R. Hunziker
• Keywords: Feature Extraction Method, ICIP 2002, Image Processing, Multiresolution Wavelet-like Algorithm, Optical Flow Algorithm