Free Online Productivity Tools
i2Speak
i2Symbol
i2OCR
iTex2Img
iWeb2Print
iWeb2Shot
i2Type
iPdf2Split
iPdf2Merge
i2Bopomofo
i2Arabic
i2Style
i2Image
i2PDF
iLatex2Rtf
Sci2ools
77
Voted
ISBI
2006
IEEE
2006
IEEE
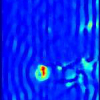
Variance controlled shear stiffness images for MRE data
In the Magnetic Resonance Elastography experiment we consider a harmonically oscillating mechanical force applied to the boundary surface of a phantom and synchronized with the motion encoding gradient. The phantom is symmetric in the direction of the applied mechanical force and the vector component in that direction decouples from the other components and satisfies a Helmholtz equation. We present a local inversion method to determine the shear wave speed that: (1) treats the phase and amplitude of the data differently; (2) computes derivatives of the data by using statistically justified filtering; and (3) varies filters according to SNR. We test our methods on data from Mayo Clinic and recover the position and stiffness of a 3mm diameter inclusion.
| Added | 20 Nov 2009 |
| Updated | 20 Nov 2009 |
| Type | Conference |
| Year | 2006 |
| Where | ISBI |
| Authors | Joyce R. McLaughlin, Daniel Renzi, Jeong-Rock Yoon, Richard L. Ehman, Armando Manduca |
Comments (0)