What is a Camera?

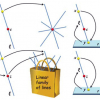
This paper addresses the problem of characterizing a general class of cameras under reasonable, “linear” assumptions. Concretely, we use the formalism and terminology of classical projective geometry to model cameras by two-parameter linear families of straight lines—that is, degenerate reguli (rank-3 families) and non-degenerate linear congruences (rank-4 families). This model captures both the general linear cameras of Yu and McMillan [16] and the linear oblique cameras of Pajdla [8]. From a geometric perspective, it affords a simple classification of all possible camera configurations. From an analytical viewpoint, it also provides a simple and unified methodology for deriving general formulas for projection and inverse projection, triangulation, and binocular and trinocular geometry.

• Type: Conference
• Year: 2009
• Where: CVPR
• Authors: Jean Ponce (Ecole Normale Superieure)
• Keywords: Computer Vision, CVPR 2009, General Linear Cameras, Linear Oblique Cameras, Stereo Vision