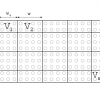
Window Annealing over Square Lattice Markov Random Field

Monte Carlo methods and their subsequent simulated annealing are able to minimize general energy functions. However, the slow convergence of simulated annealing compared with more recent deterministic algorithms such as graph cuts and belief propagation hinders its popularity over the large dimensional Markov Random Field (MRF). In this paper, we propose a new efficient sampling-based optimization algorithm called WA (Window Annealing) over squared lattice MRF, in which cluster sampling and annealing concepts are combined together. Unlike the conventional annealing process in which only the temperature variable is scheduled, we design a series of artificial ”guiding” (auxiliary) probability distributions based on the general sequential Monte Carlo framework. These auxiliary distributions lead to the maximum a posteriori (MAP) state by scheduling both the temperature and the proposed maximum size of the windows (rectangular cluster) variable. This new annealing scheme greatly enhanc...

• Type: Conference
• Year: 2008
• Where: ECCV
• Authors: Ho Yub Jung, Kyoung Mu Lee, Sang Uk Lee
• Keywords: ECCV 2008, Markov Random Field, Window Annealing