Free Online Productivity Tools
i2Speak
i2Symbol
i2OCR
iTex2Img
iWeb2Print
iWeb2Shot
i2Type
iPdf2Split
iPdf2Merge
i2Bopomofo
i2Arabic
i2Style
i2Image
i2PDF
iLatex2Rtf
Sci2ools
114
click to vote
ICIP
2006
IEEE
2006
IEEE
The Snakuscule
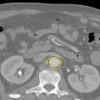
Traditional snakes, or active contours, are planar parametric curves. Their parameters are determined by optimizing the weighted sum of three energy terms: one depending on the data (typically on the integral of its gradient under the curve, or on its integral over the area enclosed by the curve), one monitoring the shape of the curve (typically promoting its smoothness, or regularizing ambiguous solutions), and one incorporating prior knowledge (typically favoring a given shape). We present in this paper a snake that we designed to be as simple as possible without losing too many of the characteristics of more complicated, fuller versions. It retains an area data term and requires regularization to avoid an ill-posed optimization problem. It is parameterized by just two points, thus further easing requirements on the optimizer. Despite its extreme simplicity, this active contour can efficiently solve a variety of problems such as cell counting and segmentation of approximately circula...
Active Contours | Area Data Term | ICIP 2006 | Ill-posed Optimization Problem | Image Processing | Planar Parametric Curves | Weighted Sum |
| Added | 22 Oct 2009 |
| Updated | 27 Oct 2009 |
| Type | Conference |
| Year | 2006 |
| Where | ICIP |
| Authors | Michael Unser, Philippe Thévenaz |
Comments (0)