Free Online Productivity Tools
i2Speak
i2Symbol
i2OCR
iTex2Img
iWeb2Print
iWeb2Shot
i2Type
iPdf2Split
iPdf2Merge
i2Bopomofo
i2Arabic
i2Style
i2Image
i2PDF
iLatex2Rtf
Sci2ools
117
click to vote
ICIP
2003
IEEE
2003
IEEE
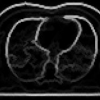
PDE-based modeling of image segmentation using volumic flooding
The classical case of morphological segmentation is based on the watershed transform, constructed by flooding the gradient image, which is seen as a topographic surface, with constant height speed. Changing the flooding criteria, (e.g constant-speed height, area or volume) yields different segmentation results. In the field of PDEs and curve evolution the classic watershed transform can be modelled as the solution of an eikonal PDE. In this paper we model the watershed segmentation based on a volume flooding criterion via a different eikonal PDE. Then we solve this PDE using the fast marching method, which is a specific algorithm from the methodology of level sets. In addition, we attempt to exploit the advantages of image segmentation using PDE-based volume flooding over the classic height flooding.
Classic Height Flooding | Flooding Criteria | ICIP 2003 | Image Processing | PDE-based Volume Flooding | Volume Flooding Criterion | Watershed Segmentation |
Related Content
| Added | 24 Oct 2009 |
| Updated | 27 Oct 2009 |
| Type | Conference |
| Year | 2003 |
| Where | ICIP |
| Authors | Anastasia Sofou, Petros Maragos |
Comments (0)