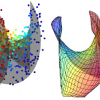
Dimensionality Reduction and Principal Surfaces via Kernel Map Manifolds

We present a manifold learning approach to dimensionality reduction that explicitly models the manifold as a mapping from low to high dimensional space. The manifold is represented as a parametrized surface represented by a set of parameters that are defined on the input samples. The representation also provides a natural mapping from high to low dimensional space, and a concatenation of these two mappings induces a projection operator onto the manifold. The explicit projection operator allows for a clearly defined objective function in terms of projection distance and reconstruction error. A formulation of the mappings in terms of kernel regression permits a direct optimization of the objective function and the extremal points converge to principal surfaces as the number of data to learn from increases. Principal surfaces have the desirable property that they, informally speaking, pass through the middle of a distribution. We provide a proof on the convergence to princ...

• Type: Conference
• Year: 2009
• Where: ICCV
• Authors: Samuel Gerber, Tolga Tasdizen, Ross Whitaker
• Keywords: Computer Vision, Dimensionality Reduction, ICCV 2009, Kernel Map Manifolds, Principal Surfaces