Free Online Productivity Tools
i2Speak
i2Symbol
i2OCR
iTex2Img
iWeb2Print
iWeb2Shot
i2Type
iPdf2Split
iPdf2Merge
i2Bopomofo
i2Arabic
i2Style
i2Image
i2PDF
iLatex2Rtf
Sci2ools
ICPR
2006
IEEE
2006
IEEE
Competitive Mixtures of Simple Neurons
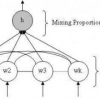
We propose a competitive finite mixture of neurons (or perceptrons) for solving binary classification problems. Our classifier includes a prior for the weights between different neurons such that it prefers mixture models made up from neurons having classification boundaries as orthogonal to each other as possible. We derive an EM algorithm for learning the mixing proportions and weights of each neuron, consisting of an exact E step and a partial M step, and show that our model covers the regions of high posterior probability in weight space and tends to reduce overfitting. We demonstrate the way in which our mixture classifier works using a toy 2-dimensional data set, showing the effective use of strategically positioned components in the mixture. We further compare its performance against SVMs and one-hidden-layer neural networks on four realworld data sets from the UCI repository, and show that even a relatively small number of neurons with appopriate competitive priors can achieve...
Competitive Finite Mixture | Computer Vision | ICPR 2006 | Mixture Classifier Works | Neurons Having Classification |
| Added | 09 Nov 2009 |
| Updated | 09 Nov 2009 |
| Type | Conference |
| Year | 2006 |
| Where | ICPR |
| Authors | Karthik Sridharan, Matthew J. Beal, Venu Govindaraju |
Comments (0)