Nonlinear classification of EEG data for seizure detection

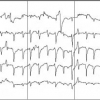
We address the problem of classification of EEG recordings for the detection of epileptic seizures. We assume that the EEG measurements can be described by a low dimensional manifold. The geometry of the manifold is typically nonlinear and can be recovered with the Laplacian Eigenmaps method. Our experiments demonstrate that the manifold can reveal the intrinsic structure of the data and that baseline and ictal states are well separated. We use a Kernel Ridge Regression to identify the boundary between ictal and baseline states. We have performed a quantitative evaluation of our new approach using an acute rat model of epilepsy. Our experiments show that our approach outperforms PCA combined with a kernel ridge classifier.

• Type: Conference
• Year: 2006
• Where: ISBI
• Authors: Mabel Ramírez-Vélez, Richard Staba, Daniel S. Barth, François G. Meyer
• Keywords: ISBI 2006, Kernel Ridge Classifier, Kernel Ridge Regression, Low Dimensional Manifold, Medical Imaging