Free Online Productivity Tools
i2Speak
i2Symbol
i2OCR
iTex2Img
iWeb2Print
iWeb2Shot
i2Type
iPdf2Split
iPdf2Merge
i2Bopomofo
i2Arabic
i2Style
i2Image
i2PDF
iLatex2Rtf
Sci2ools
129
Voted
CVPR
2008
IEEE
2008
IEEE
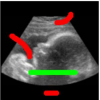
Interactive image segmentation via minimization of quadratic energies on directed graphs
We propose a scheme to introduce directionality in the Random Walker algorithm for image segmentation. In particular, we extend the optimization framework of this algorithm to combinatorial graphs with directed edges. Our scheme is interactive and requires the user to label a few pixels that are representative of a foreground object and of the background. These labeled pixels are used to learn intensity models for the object and the background, which allow us to automatically set the weights of the directed edges. These weights are chosen so that they bias the direction of the object boundary gradients to flow from regions that agree well with the learned object intensity model to regions that do not agree well. We use these weights to define an energy function that associates asymmetric quadratic penalties with the edges in the graph. We show that this energy function is convex, hence it has a unique minimizer. We propose a provably convergent iterative algorithm for minimizing this ...
Computer Vision | Convergent Iterative Algorithm | CVPR 2008 | Energy Function | Object Boundary Gradients | Object Intensity Model | Random Walker Algorithm |
Related Content
| Added | 12 Oct 2009 |
| Updated | 28 Oct 2009 |
| Type | Conference |
| Year | 2008 |
| Where | CVPR |
| Authors | Dheeraj Singaraju, Leo Grady, René Vidal |
Comments (0)