How To Deal with Point Correspondences and Tangential Velocities in the Level Set Framework

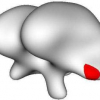
In this paper, we overcome a major drawback of the level set framework: the lack of point correspondences. We maintain explicit backward correspondences from the evolving interface to the initial one by advecting the initial point coordinates with the same speed as the level set function. Our method leads to a system of coupled Eulerian partial differential equations. We show in a variety of numerical experiments that it can handle both normal and tangential velocities, large deformations, shocks, rarefactions and topological changes. Applications are many in computer vision and elsewhere since our method can upgrade virtually any level set evolution. We complement our work with the design of non zero tangential velocities that preserve the relative area of interface patches; this feature may be crucial in such applications as computational geometry, grid generation or unfolding of the organs' surfaces, e.g. brain, in medical imaging.

• Type: Conference
• Year: 2003
• Where: ICCV
• Authors: Jean-Philippe Pons, Gerardo Hermosillo, Renaud Keriven, Olivier D. Faugeras
• Keywords: Computer Vision, Explicit Backward Correspondences, ICCV 2003, Level Set Evolution, Level Set Framework, Level Set Function, Tangential Velocities