Compatible Triangulations of Spatial Decompositions

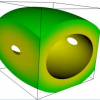
We describe a general algorithm to produce compatible 3D triangulations from spatial decompositions. Such triangulations match edges and faces across spatial cell boundaries, solving several problems in graphics and visualization including the crack problem found in adaptive isosurface generation, triangulation of arbitrary grids (including unstructured grids), clipping, and the interval tetrahedrization problem. The algorithm produces compatible triangulations on a cell-by-cell basis, using a modified Delaunay triangulation with a simple point ordering rule to resolve degenerate cases and produce unique triangulations across cell boundaries. The algorithm is naturally parallel since it requires no neighborhood cell information, only a unique, global point numbering. We show application of this algorithm to adaptive contour generation; tetrahedrization of unstructured meshes; clipping and interval volume mesh generation. CR Categories: I.3.5 [Computing Methodologies]: Computer Graphic...

• Type: Conference
• Year: 2004
• Where: VIS
• Authors: Berk Geveci, Mathieu Malaterre, William J. Schroeder
• Keywords: Compatible 3D Triangulations, Compatible Triangulations, Triangulations Match Edges, VIS 2004, Visualization