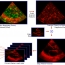
Volterrafaces: Discriminant Analysis using Volterra Kernels

In this paper we present a novel face classification system where we represent face images as a spatial arrangement of image patches, and seek a smooth non-linear functional mapping for the corresponding patches such that in the range space, patches of the same face are close to one another, while patches from different faces are far apart, in L2 sense. We accomplish this using Volterra kernels, which can generate successively better approximations to any smooth non-linear functional. During learning, for each set of corresponding patches we recover a Volterra kernel by minimizing a goodness functional defined over the range space of the sought functional. We show that for our definition of the goodness functional, which minimizes the ratio between intra-class distances and inter-class distances, the problem of generating Volterra approximations, to any order, can be posed as a generalized eigenvalue problem. During testing, each patch from the test image that is class...

• Type: Conference
• Year: 2009
• Where: CVPR
• Authors: Ritwik Kumar, Arunava Banerjee, Baba C. Vemuri
• Keywords: Computer Vision, CVPR 2009, Volterra Kernels, Volterrafaces